Discrete Random Variables
Flip a fair coin three times. What's the probability that we'll get at least two heads?
The number of times we get heads will be our random variable and given three flips of a fair coin the possible outcomes are,
\[ S = \{ HHH, HHT, HTT, HTH, THT, THH, TTH, TTT \}\,. \]We can see that of these possibilities, \(HHH\), \(HHT\), \(HTH\), and \(THH\) will yield at least two heads which is four of the eight total potential outcomes, or a probability of \(\frac{1}{2}\).
We can plot the probability distribution to visually show the possible outcomes. The \(x\) axis is numbered with \(0\), \(1\), \(2\), and \(3\), where each number is the number of heads in the three flips. The \(y\) axis is the number of times that value arose given three flips. For example, \(0\) heads comes up once, when we flip tails three times. Similarly, three heads comes up once, when we flips heads three times. The rest of the possibilities are combinations of 1 and 2 or 2 and 1 for heads and tails.
X = [ 0, 1, 2, 3 ];
Y = [ 1, 3, 3, 1 ];
bar(X, Y)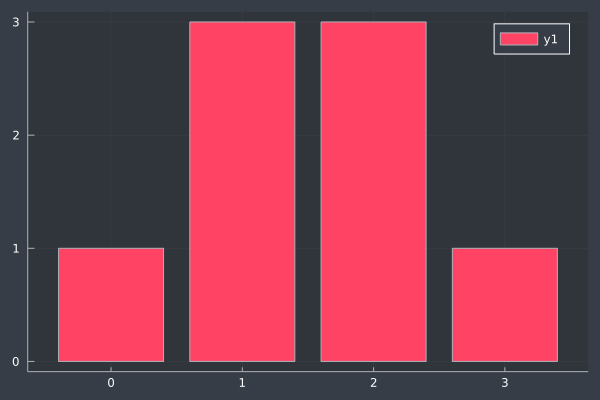
Is there a better way for us to determine the number of possible cases rather than manually writing them all out? Sure is!
\[ \text{number of cases}^\text{number of flips}\]In this situation, we're dealing with two cases – heads or tails. And we're flipping the coin three times, therefore \(2^3 = 8\). Suppose we wanted to know the number of possible outcomes if we were to flip the same fair coin five times, \( 2^5 = 32 \).