Basic Probability Rules
The field of probability is all about transforming counts of possible outcomes into geometric areas, volumes, etc.
Let \(S\) be a set called the sample space. Each element of \(S\) is called an event, \(E\). The events each have a value which ranges from \(0\) to \(1\) and all the elements of \(S\) must sum to \(1\).
Suppose we're rolling a fair die. There are six, discrete outcomes – I could roll a number anywhere from \(1\) to \(6\) and each outcome is equally likely. Suppose we rolled the die some arbitrary number of times and we saw that the distribution was not \(\frac{1}{6}\)th for each outcome. We would conclude that the die was weighted, or otherwise known as not fair.
Let's see what happens when we're working with an unfair set of dice. We can write a function for a fair die.
function rollfairdie()
rand(1:6)
end
function sumfrequencies(samplespace, events)
frequencies = zeros(Float64, length(samplespace))
for evt in events
frequencies[evt] += 1
end
frequencies
endHere we're generating a random integer between one and six, equally.
rolls = 100
events = [ rollfairdie() for _ in 1:rolls ];
probabilities = map(x -> x/rolls, sumfrequencies(collect(1:6), events))
bar(1:6, probabilities, legend=:topleft, label="Probabilitiy")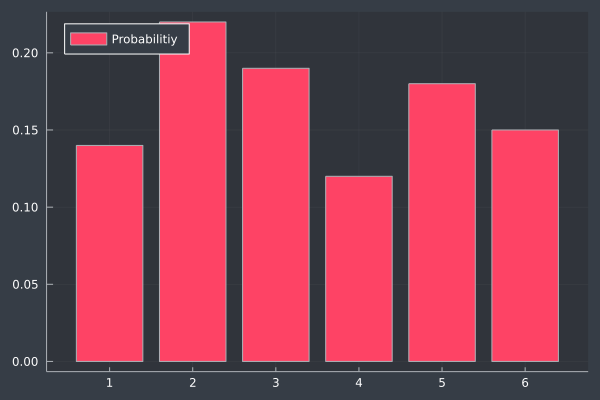
Given one-hundred rolls, we can see that the distribution is fairly evenly spread across each of the numbers one through six.
Now we'll use a feature from the StatsBase package – sample and Weight. sample takes two vectors, one is going to be the sample space, e.g. \(1\) to \(6\). The second one is the Weight object which contains a associated value for each element in the first vector – the weight.
function rollweighteddie(; wts=Weights([1, 1, 1, 1, 6, 6]))
sample(1:6, wts)
end
rolls = 100
wts = Weights([1, 1, 1, 1, 6, 6])
events = [ rollweighteddie(wts=wts) for _ in 1:rolls ];
probabilities = map(x -> x/rolls, sumfrequencies(collect(1:6), events))
bar(1:6, probabilities, legend=:topleft, label="Probability")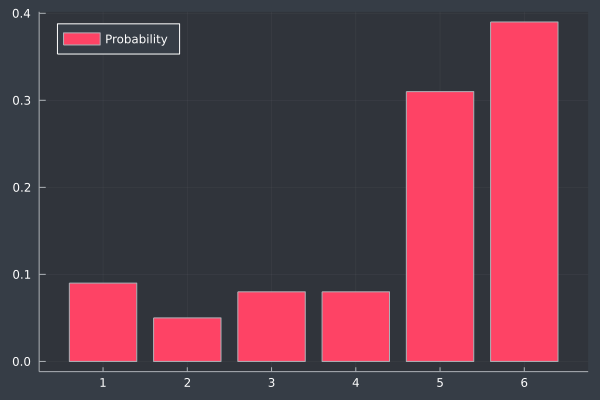
Now we can see that since we've weighted the die with an higher likelihood of rolling a 5 or 6, and the plot shows us just that.
Independence
Suppose that we have two events such as I roll a die twice.