Lattice Paths (PE15)

The 15th problem on Project Euler states,

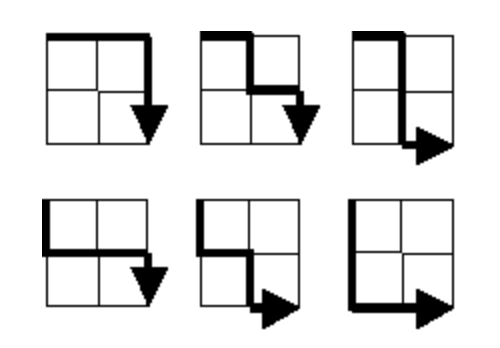
"Starting in the top left corner of a 2×2 grid, and only being able to move to the right and down, there are exactly 6 routes to the bottom right corner."

Finally, it poses the question, "How many such routes are there through a 20×20 grid?"

There are lots of ways to programmatically find the solution to this problem, however there's no good reason to waste the cycles when we can easily apply mathematics.

We use the "\(n\) choose \(k\)" tool from combinatorics which is defined as,

\[\binom{n}{k} = \frac{n!}{k!(n-k)!}\,.\]

This formula tells us the number of different ways we can select \(k\) elements from \(n\) total elements.

Let's take the simple example we are given first, that of a \(2 \times 2\) grid. Why are there six possible routes?

At each new position, we can branch in two possible ways, down or right. This means that we want to know how many ways can move given a total of 2 possible movements? Therefore, for any grid of \(n \times n\), we have the formula,

\[\binom{2n}{n}\,.\]

To solve the problem, we use Julia's binomial function from the standard library.

n = 20
@time binomial(2n, n)

>   0.000001 seconds
> 137846528820